 PHIL 1423
PHIL 1423
Introduction à la logique
 PHIL 1423
PHIL 1423
La séance du 20 mars était particulièrement «corsée».
Nous y avons abordé trois thèmes:
Le concept de forme normale disjonctive La notation polonaise Méthode sémantique vs. méthode syntaxique
- La méthode qui emploie des tables de vérité (matrices) est une méthode dite sémantique; les méthodes s'appuyant sur l'axiomatique et la déduction naturelle sont considérées comme des méthodes syntaxiques.
Le concept de forme normale disjonctive
La forme normale disjonctive a étéprésentée (sans que le terme soit employé) àla séance précédente lorsque nous avons analysél'énoncé
«[(P &Q)R]
P »en nous servant de la méthode ramifiée de Smullyan, pour découvrir que l'énoncé«[(P &Q)
R]
P »est, en fait, l'équivalent de l'énoncé
« (P &
Q) v (P & R) »
Cet énoncé est une disjonction des différentes manières (pour ainsi dire) dont
« [(P & Q)R]
P » peut être vrai. Il s'agit de la forme normale disjonctive minimale de « [(P & Q)
R]
P ».
La forme normale disjonctive d'un énoncé X est un énoncé Y ayant la même table de vérité que X et composé de la disjonction d'une série de conjonctions ayant une propriété particulière - celle d'être composées uniquement d'énoncés élémentaires ou d'énoncés qui sont la négation d'un énoncé élémentaire. La forme normale disjonctive est dite « pleine » lorsque chaque membre de la disjonction (chaque conjonction) contient tous les énoncés élémentaires dont est composé l'énoncé X.
Ainsi, la forme normale disjonctive de « P v Q » (forme pleine) serait donc :
(P & Q) v ((P &
Q) v (
P & Q))
que l'on se permet d'écrire :
(P & Q) v (P &
Q) v (
P & Q).
Cette forme est la forme pleine, puisque chacune des trois conjonction -- il s'agit de «(P&Q)», «(P&
Q)» et «(
P&Q)») -- contient P ou la négation de P, ainsi que Q ou la négation de Q. La forme normale disjonctive minimale de « P v Q » est, tout simplement:
P v Q
Pour donner un autre exemple, la forme normale disjonctive pleine de « P
Q » serait :
(P & Q) v (
P & Q) v (
P &
Q)
Cette forme se lit sur la table de vérité de « P
Q ».
P Q P Q
v v v v f f f v v f f v Cette table, en effet, indique que « P
Q » est vrai si P et Q sont vrais,
que « PQ » est vrai si P est faux et Q vrai et que « P
Q » est vrai si P et Q sont faux tous les deux. La forme normale disjonctive ne fait qu'affirmer la disjonction de ces trois possibilités, indiquées par les trois lignes de la table de vérité où « P
Q » prend la valeur « vrai ».
La forme normale disjonctive minimale de « P
Q » est
P v Q
La forme normale disjonctive pleine
(P &Q) v (P &Q) v (
P &
Q)
de «PQ »
peut être convertie en la forme normale disjonctive minimale de la façon suivante:
(P & Q)v (
P &Q) v (
P &
Q)
devient, successivement, puisque XvYvZ est équivalent àYvZvX, àYvZvXvY et à[YvZ]v[XvY]:
(
P &Q) v (
P &
Q) v (P & Q)
(
P & Q) v (
P &
Q) v (P &Q) v (
P & Q)
[(
P &Q) v (
P &
Q)]v [(P &Q) v (
P &Q)]
Ce dernier énoncédevient àson tour (en transformant «P &Q »en
«Q &P »et «P &Q »en «Q &
P ».
[(
P &Q) v (
P &
Q)]v [(Q & P) v (Q &
P)]
L'énoncése voit maintenant comme une disjonction dont les deux membres sont enfermés entre crochets ([, ]). Le premier membre est équivalent à
P&(Qv
Q) donc à
P et le deuxième membre est équivalent àQ&(Pv
P) donc àQ. On écrit donc:
P v Q
comme forme normale disjonctive minimale. La méthode ramifiée de Smullyan, appliquée àun seul énoncé, nous permet toujours de trouver une forme disjonctive de l'énoncéqui est analysé. Il s'agit de la disjonction de ce que disent les embranchements non encore fermés àla fin de l'analyse. (Ce qu'un embranchement «dit»se découvre en faisant la conjonction des énoncés élémentaires et de leurs négations qui s'y découvrent en remontant du bout de la branche vers le haut.) Cette forme disjonctive que l'on découvre par le moyen de la méthode de Smullyan sera tantôt la forme normale disjonctive minimale, tantôt la forme disjonctive normale pleine et tantôt une forme intermédiaire entre les deux.
La notation polonaise
Inventée par des logiciens polonais (d'oùle nom), cette forme de notation permet d'éviter les parenthèses. Voici quelques exemples d'énoncés exprimés dans cette notation, avec les équivalents dans la notation que nous avons employée jusqu'ici.
P s'écrit p s'écrit q P
s'écrit Np Q
s'écrit Nq s'écrit Kpq s'écrit Apq Q)
s'écrit Cpq Q)
s'écrit Epq P &
Q)
s'écrit KNpNq (P & Q)
s'écrit NKpq (P &
Q)
s'écrit NKpNq Q)
(
Q
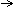
P)
s'écrit CCpqCNqNp 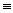
(
P v
Q)
s'écrit EKpqNANpNq P
s'écrit CKpqq R]
[P
(Q
R)]
s'écrit CCKpqrCpCqr
- Qu'est-ce qu'un axiome?
- Qu'est-ce qu'un théorème? (Introduction du symbole
.)
En réponse à une question, nous avons abordé un peu
l'histoire de la notion d'axiome. Pour les fins de notre système
SP, un axiome est tout simplement un énoncé qui correspond
à l'un ou à l'autre des trois schémas donnés sur
la feuille distribuée en classe. Ce sont des énoncés
que nous avons décidé d'accepter comme «vrais»,
mais sans nous imposer la nécessité de les démontrer
ou de les prouver.
Pour Euclide, par contre, les «axiomes» de sa géométrie avaient non seulement le statut d'énoncés que l'on n'avait pas besoin de prouver -- mais ils avaient en outre le statut de vérités. Il s'agissait en outre de «vérités» que l'esprit rationnel reconnaissait tout de suite comme vraies, sans aucune nécessité de les prouver. La découverte des géométries non euclidiennes nous a permis d'en venir à une conception beaucoup plus relativisée du statut des axiomes d'un système.