 PHIL 1423
PHIL 1423 Introduction à la logique
 PHIL 1423
PHIL 1423
Quelques équivalences utiles (et nécessaires) pour bien appliquer la méthode ramifiée de Smullyan
Nous avons repéré les équivalences suivantes, très utiles dans le contexte de la méthode de Smullyan, voire même nécessaires afin de décomposer les énoncés complexes dont le foncteur principal n'est ni & ni v:

X
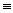
X Y)
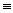
( X v Y)
Y)
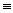
[(X Y) & (Y
X)]
Y)
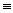
[(X & Y) v ( X &
Y)]
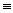
[(X v Y) & (X & Y)]
(X
Y)
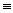
[
(X &
Y)]
(X
Y)
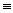
(X & Y)
(X &Y)
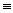
( X v
Y)
(X v Y)
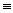
( X &
Y)
(X
Y)
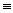
(X v Y)
Révision de la méthode ramifiée de Smullyan (suite)
Il s'ensuit de là que « [(P & Q) ![]() R]
R] ![]() P » est équivalent à « (
P » est équivalent à « (![]() Q & P) v (R & P) » ou, ce qui revient au même, «
(P &
Q & P) v (R & P) » ou, ce qui revient au même, «
(P & ![]() Q) v (P & R) ».
Q) v (P & R) ».
On peut construire une table de vérité pour confirmer l'exactitude de ce résultat, comme nous l'avons fait d'ailleurs en classe.
Les détails suivants (en caractères violets) sont fournis par anticipation (n'ayant pas été présentés à la séance du 15 mars):
La forme normale disjonctive de «
[(P & Q) ![]() R]
R] ![]() P » que l'on vient de donner n'est pas la
forme pleine,
mais bien ce que nous appellerons la forme
minimale.
P » que l'on vient de donner n'est pas la
forme pleine,
mais bien ce que nous appellerons la forme
minimale.
La forme pleine de « (P & ![]() Q) v (P & R) » est obtenue de la manière
suivante :
Q) v (P & R) » est obtenue de la manière
suivante :
Nous voyons que la méthode de Smullyan
nous donne une recette permettant de trouver assez rapidement la forme
normale disjonctive de n'importe quel énoncé non contradictoire.
Mais il s'agit de la forme normale disjonctive minimale, non pas de la forme
normale disjonctive pleine.