PHIL 1423
Introduction à la logique

La méthode ramifiée de Smullyan
pour l'évaluation de la validité des raisonnements (et pour la détection de contradictions)

 
1) L'idée générale sur laquelle s'appuie la méthode

Cette méthode s'appuie sur la troisième des trois définitions de la notion de validité déductive que nous avons étudiées et selon laquelle un raisonnement est valide si et seulement si « il y a contradiction à affirmer les prémisses en niant la conclusion ».

La méthode ramifiée de Smullyan commence donc par faire une liste des prémisses et de la négation de la conclusion.

Pour évaluer le raisonnement

e₁
e₂
...
e_n
______________
 
donc, e_c


on fait la liste suivante :
 

 e₁
 e₂
 ...
 e_n
¬e_c


Par cette liste, nous affirmons les prémisses du raisonnement qui est à évaluer et nous en nions la conclusion.  Le dernier élément de la liste sera donc non pas la conclusion elle-même mais plutôt la négation de la conclusion.

La méthode ramifiée de Smullyan (dont les autres étapes seront expliquées en classe) consiste à détecter les contradictions dans cette liste (s'il en existe).

Elle consiste à se poser la question de savoir si les prémisses et la négation de la conclusion peuvent être vraies simultanément, sans qu'il y ait contradiction.  Si les prémisses et la négation de la conclusion ne peuvent pas être vraies simultanément, nous considérons que le raisonnement est valide.
 
 

---

 
 
 

2) Techniques d'analyse employées par la méthode.
 
2a) Le cas d'un énoncé dont le principal foncteur est v (disjonction inclusive) :
 
 
 
Ici, chaque embranchement indique l'une des possibilités qui permettrait à l'énoncé
« X v Y» d'être vrai. 

---

2b) Le cas d'un énoncé dont le principal foncteur est & (conjonction) :
 
 
 

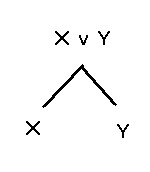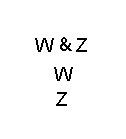Ici, il n'y a pas d'embranchement.  L'arbre n'a qu'un «tronc» pour ainsi dire.    En remontant le tronc, on découvre que W doit être vrai, puis Z doit être vrai pour que « W & Z » puisse être vrai.

---


 
 
 
2c) Le cas d'un énoncé dont le principal foncteur est  (négation).
 
Ici, deux cas sont possibles:
(i) Il s'agit d'un énoncé qui commence par une double négation ().  Dans ce cas, on élimine la double négation et on inscrit le résultat.
(ii) Il s'agit d'un énoncé qui est tout simplement la négation d'un énoncé élémentaire (P, par exemple, est la négation de P).  Dans ce cas, on laisse l'énoncé tel quel.
(iii) Il s'agit de la négation d'un énoncé complexe.  Dans ce cas, il faut essayer de transformer l'énoncé en un énoncé équivalent qui ne commence pas par .   On peut se servir, par exemple, des lois de De Morgan
• Dans l'example suivant, «  (P & Q) » est transformé  en «  P v Q » par la loi de De Morgan, puis en «  P v Q » par l'élimination d'une double négation.  «  P v Q », par la suite, pourra être traité comme une disjonction ordinaire.

 
 
• Les deux embranchements de cette analyse montrent les deux possibilités qui rendent notre énoncé de départ «  (P & Q) » vrai.  Il sera vrai, en somme, si P est vrai ou encore si Q est vrai (ou encore, mais cela va sans dire, si les deux sont vrais).

---

2d) Le cas où l'on a deux ou plusieurs énoncés à analyser :
 
Quand on a deux ou plusieurs énoncés à analyser on peut commencer par analyser n'importe lequel d'entre eux.  Afin d'éviter la confusion, nous cocherons chaque ligne qui a été traité, pour ainsi dire.  L'example suivant, par exemple, indique la première étape de l'analyse des deux énoncés X&Y et ZvW.  Le fait que l'on ait commencé par analyser X&Y est indiqué par le fait que X&Y est coché.
 
 
 

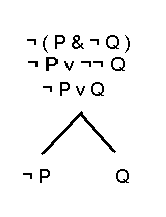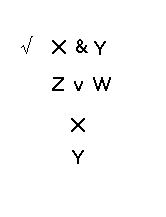Voici maintenant la deuxième étape de cette analyse :
 
 
 

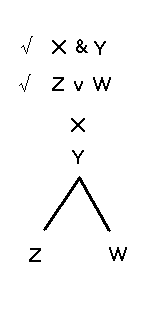Cette analyse indique (par ses deux embranchements) qu'il existe deux combinaisons qui rendent vrais les deux énoncés X&Y et ZvW, soit la vérité de Z, Y et X et la vérité de W, Y et X.

Mais nous aurions pu, tout aussi bien, commencer par analyser ZvW.  Dans ce cas, la première étape de l'analyse serait la suivante :
 
 
 

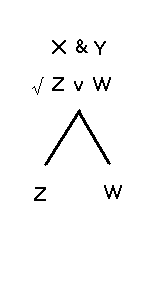Et la deuxième étape serait :
 
 
 

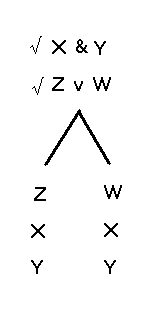Encore une fois, on voit, par les deux embranchements de notre analyse, qu'il y a deux combinaisons possibles qui rendent vrais les énoncés X&Y et ZvW, soit la vérité de Y, X et Z et la vérité de Y X et W.
 

---

 

 
3) Application de ces techniques pour détecter les contradictions.
 
On ferme un embranchement de l'arbre en y inscrivant un X dès que l'on y détecte une contradiction.  Un embranchement contient une contradiction si, en remontant du bout de l'embranchement vers le début de la liste des énoncés, on rencontre un énoncé e et la négation du même énoncé ¬e.

On poursuit l'analyse jusqu'à ce que tous les embranchements soient fermés -- auquel cas on a prouvé qu'il est contradictoire d'affirmer en même temps l'ensemble des énoncés analysés -- ou (au cas où tous les embranchements ne se referment pas) jusqu'à ce que tous les énoncés complexes aient été cochés et qu'il ne reste plus que des propositions élémentaires (P, Q, R, etc.) et la négation de propositions élémentaires (¬P, ¬Q, ¬R, etc.)
 

---

 

 

4) En résumé
 
Pour tester la validité d'un raisonnement on suit les étapes suivantes:
 
1. On fait une liste des prémisses du raisonnement et de la négation de la conclusion.
2. On en fait une analyse en utilisant la méthode ramifiée de Smullyan expliquée ci-dessus.
3. On observe si tous les embranchements se ferment ou non.
4. Si tous les embranchements se ferment, cela veut dire que l'on se contredit en affirmant les prémisses et en niant la conclusion.  En d'autres mots, le raisonnement est valide.

S'il existe des embranchements qui, à la fin de l'analyse, ne sont pas fermés, cela prouve qu'il est possible que la conclusion soit fausse alors que les prémisses sont vraies, c'est-à-dire que le raisonnement est invalide.
Pour de plus amples explications, on peut se référer à ses notes de cours.