 PHIL
1423
Introduction à la
logique
PHIL
1423
Introduction à la
logique
Points saillants de la séance du mardi
5 février 2002
Mise à jour du 19 février et du 14 avril 2002.
Pour retourner à la liste
des séances, cliquer ici.
Pour retourner à la page
d'accueil du cours, cliquer ici.
-
Révision de l'exercice no 7.
-
Distribution de l'exercice no 8
(pour vendredi).
-
Les seize fonctions de vérité possibles (à deux
variables)
| P |
Q |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| v |
v |
v |
f |
v |
f |
v |
f |
v |
f |
v |
f |
v |
f |
v |
f |
v |
f |
| v |
f |
v |
v |
f |
f |
v |
v |
f |
f |
v |
v |
f |
f |
v |
v |
f |
f |
| f |
v |
v |
v |
v |
v |
f |
f |
f |
f |
v |
v |
v |
v |
f |
f |
f |
f |
| f |
f |
v |
v |
v |
v |
v |
v |
v |
v |
f |
f |
f |
f |
f |
f |
f |
f |
|
|
P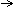 P P |
P Q Q |
P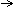 Q Q |
 P P |
Q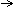 P P |
 Q Q |
P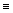 Q Q |
P Q Q |
PvQ |
PvQ |
Q |
 P&Q P&Q |
P |
P& Q Q |
P&Q |
Q& Q Q |
|
|
tau-
to-
lo-
gie |
pas
à la
fois(*) |
|
|
|
|
|
ni...
ni...(*) |
|
|
Q |
|
P |
|
|
con-
tra-
dic-
tion |
*NOTE : Ces foncteurs (symbolisés  et
et  ) portent le nom de barre
de Sheffer («Sheffer stroke») et flèche de Peirce en
mémoire des logiciens H. M. Sheffer et C. S. Peirce qui les ont
découverts et analysés. Le foncteur
) portent le nom de barre
de Sheffer («Sheffer stroke») et flèche de Peirce en
mémoire des logiciens H. M. Sheffer et C. S. Peirce qui les ont
découverts et analysés. Le foncteur  peut s'appeler « barre d'incompatibilité ».
peut s'appeler « barre d'incompatibilité ».
Nous avons élaborés une recette mécanique qui permet
de produire, à partir d'une table de vérité donnée,
un énoncé qui a comme table de vérité précisément
celle-là.
Des ensembles de foncteurs complets :
-
{
 , & }, {
, & }, { ,
v }, {
,
v }, { ,
, 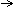 }, {
}, {  }, {
}, {  }
}
-
Des ensembles de foncteurs incomplets :
-
{
 , v }, {
, v }, { ,
, 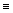 }
}
-
-
Ce n'est pas un exercice en tant que tel, mais de dire
pourquoi
les deux ensembles de foncteurs précédents sont incomplets,
c'est-à-dire pourquoi il est impossible en se limitant à
ces foncteurs de construire des énoncés correspondant aux
16 tables de vérité possibles avec deux variables!!
Les lois de De Morgan :
-
 (P & Q)
(P & Q) 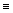 (
( P v
P v  Q)
Q)
-
 (P v Q)
(P v Q) 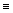 (
( P &
P &  Q)
Q)
-
(P & Q)
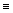
 (
( P
v
P
v  Q)
Q)
-
(P v Q)
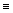
 (
( P
&
P
&  Q)
Q)
-
Pas de D5M, faute de temps, mais il est possible de soumettre une
D5M facultative au début du cours de vendredi.
 PHIL
1423
PHIL
1423
 PHIL
1423
PHIL
1423
et
) portent le nom de barre de Sheffer («Sheffer stroke») et flèche de Peirce en mémoire des logiciens H. M. Sheffer et C. S. Peirce qui les ont découverts et analysés. Le foncteur
peut s'appeler « barre d'incompatibilité ».